Jonathan Poholarz

Many strategy games take place on a gridded map, and, often, these maps are intended to represent some sort of world. Of course, as map makers have struggled to do for centuries, representing a globe on a flat map is never perfect.
With this in mind, I wanted to experiment with possible ways to instead represent a 2D map as a sphere. In the context of a strategy games, this makes the poles of a map more relevant and accurately sized, not stretched to unreasonable proportions like the well known Mercator projection.
I've experimented with a couple different approaches to tiling a sphere. The goal is to cover its surface with regular tiles of roughly the same size. The first attempt begins with a cube where each of a cube's eight points are located on a unit sphere. Then, each square face of the cube is divided into 4 smaller squares and each point displaced to lie on the unit sphere. This process can be repeated as many times as desired until enough tiles have been created.
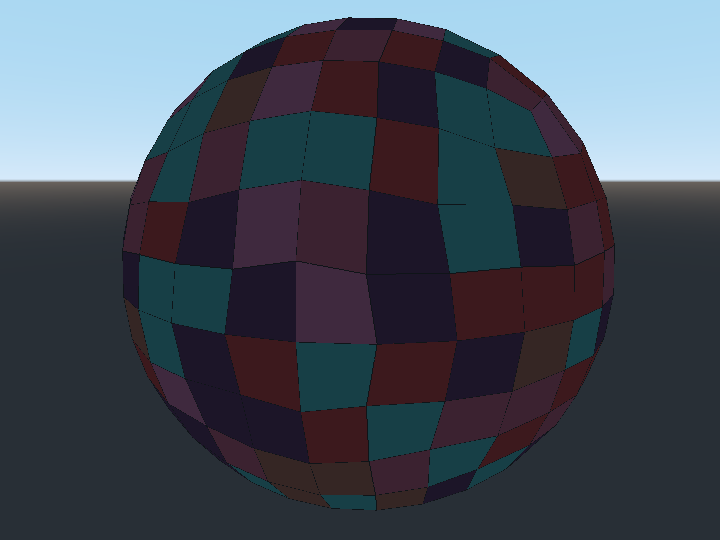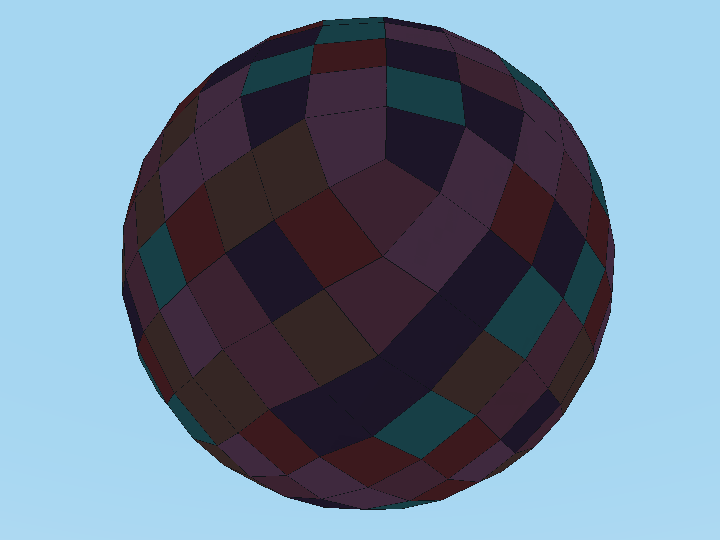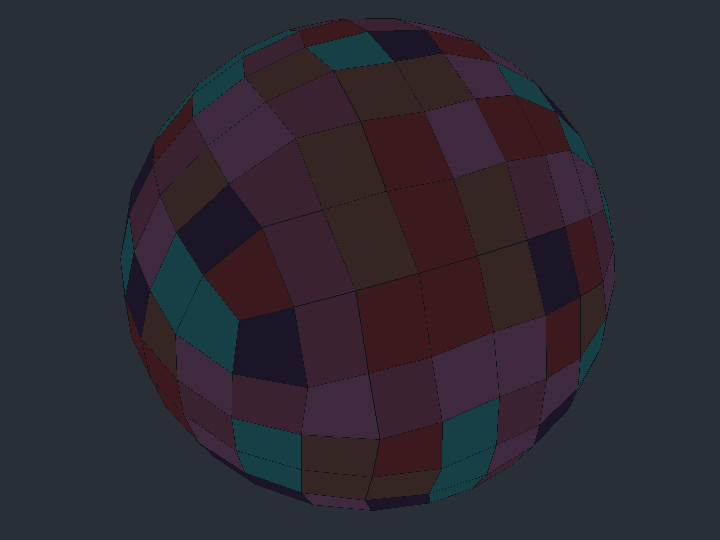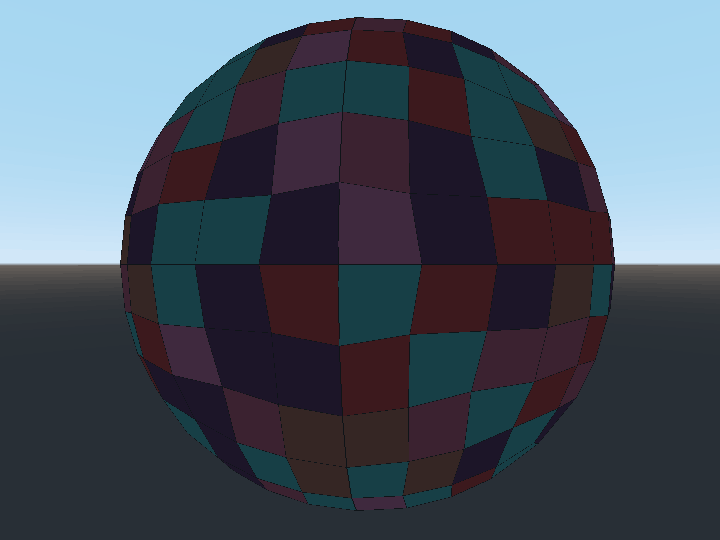
Although pretty easy, some of the tiles in this method do sort of lose their square shape. Additionally, square tiles do suffer from other strategic disadvantages, namely the fact that diagonal movement either moves someone sqrt(2) units in one move or isn't allowed, requiring instead units of movement to go sqrt(2) distance.
This is where hexagonal grids typically come into play, having equidistant movement in all directions. However, there is no regular geometric solid that can be created with only hexagons. Instead, I experimented with just triangles, since a hexagon is in fact made of 6 triangles.
Starting with an icosahedron (one of those D20 dice for reference), I can apply a similar subdivision strategy as I did with the cube. I start with a 20 sided die of triangles where each point is close to the unit sphere. Then each triangular side is divided into 4 smaller triangles and the points of those triangles adjusted to lie on the desired sphere. Then, of course, this can be repeated many times.
While this has been a rather rough first attempt and exploration of the idea of working with a sphere, it has been a good learning experience with the algorithms and some of the basics of the Godot Engine's 3D capabilities. There are definitely things that can be optimized and done better than I'm doing them of course, as my framerate will quickly drop after about 4 subdivisions (5120 triangles).
I would also like to explore working with shaders to color the tiles so that the globe looks more like a planet rather than rainbow colored shapes, but that will come in a future project.